电路布线
题目描述:
在解决电路布线问题时,一种很常用的方法就是在布线区域叠上一个网格,该网格把布线区域划分成m*n个方格,布线时,转弯处必须采用直角,如已经有某条线路经过一个方格时,则在该方格上不允许叠加布线。如下图所示,如从一个方格a(2,1)的中心点到另一个方格b(8,8)的中心点布线时, 每个方格布线时需要1个单位的电路材料,所需要最少的电路材料是16。
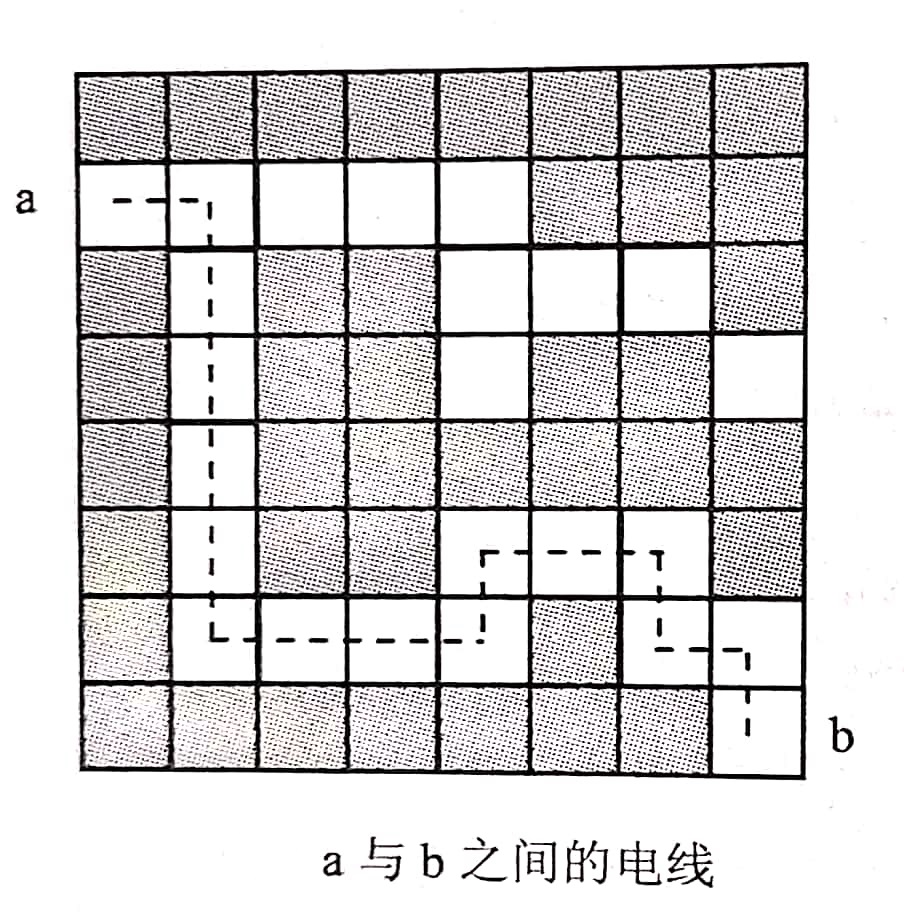
输入描述:
第一行输入网格的m和n
第二行开始输入网格中已经布线的情况,如果已经有布线时,用1表示,尚未布线时,用0表示。
接下来两行分别输入需要布线的起始位置a和结束位置b。
输出描述:
输出从起始位置a到结束位置b布线时所需要的最少电路材料。
输入样例:
8 8
1 1 1 1 1 1 1 1
0 0 0 0 0 1 1 1
1 0 1 1 0 0 0 1
1 0 1 1 0 1 1 0
1 0 1 1 1 1 1 1
1 0 1 1 0 0 0 1
1 0 0 0 0 1 0 0
1 1 1 1 1 1 1 0
2 1
8 8
输出样例:
16
解题思路:
不想自定义结构体,那就先用pair<int,int>来表示一个坐标点吧。用G来表示迷宫地图,其中1为通 0为不通。用vis来判断迷宫地图中的坐标是否被访问过。用一个pair型的二维数组来记录(i,j)坐标的前一个坐标。先用一个queue来进行广度优先搜索 记录所有能走通的坐标的前一个坐标。用ans来记录从起点a到终点b所需的最少电路材料,然后从终点坐标b开始进行回溯,一直回溯到起点为止,最后输出ans即可。
AC代码:
#include <bits/stdc++.h>
using namespace std;
#define Up(i,a,b) for(int i = a; i <= b; i++)
#define ms(a,x) memset(a,x,sizeof(a))
#define P pair<int,int>
#define mp(x,y) make_pair(x,y)
const int INF = 0x3f3f3f3f; //无穷大
const int maxn = 505;
int G[maxn][maxn]; //迷宫地图,G[i][j]=1为通,0为不通
bool vis[maxn][maxn]; //判断vis[i][j]是否被访问过
P pre[maxn][maxn]; //pre[i][j]表示走到(i,j)的前一步
int main()
{
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
int m,n;
cin >> m >> n;
ms(G,-INF);
ms(vis,false);
Up(i,1,m)
{
Up(j,1,n)
{
cin >> G[i][j];
}
}
P a,b; //起点坐标a,终点坐标b
cin >> a.first >> a.second >> b.first >> b.second;
queue<P> q;
q.push(a);
while(!q.empty())
{
P cur = q.front();
q.pop();
int x = cur.first, y = cur.second;
vis[x][y] = true;
if(x==m && y==n)
{
break;
}
if(x>1 && !vis[x-1][y] && !G[x-1][y]) //若G[x-1][y]=1且该点未被访问过
{
q.push(mp(x-1,y));
pre[x-1][y] = cur;
}
if(y>1 && !vis[x][y-1] && !G[x][y-1])
{
q.push(mp(x,y-1));
pre[x][y-1] = cur;
}
if(x<m && !vis[x+1][y] && !G[x+1][y])
{
q.push(mp(x+1,y));
pre[x+1][y] = cur;
}
if(y<n && !vis[x][y+1] && !G[x][y+1])
{
q.push(mp(x,y+1));
pre[x][y+1] = cur;
}
}
int ans = 1; //从a到b所需的最少电路材料
P cur = b; //从终点开始回溯
while(cur.first!=a.first || cur.second!=a.second) //直到回溯到起点为止
{
ans++;
cur = pre[cur.first][cur.second];
}
cout << ans << endl;
return 0;
}

























还没有任何评论,你来说两句吧!